LCM and HCF Formulas, Shortcuts and Tricks with Examples

LCM and HCF Formulas, Shortcuts and Tricks with Examples

LCM and HCF Short Tricks with Examples

Factors and Multiples:

• If number p divided another number q exactly, we say that p is a factor of q.
• In this case, q is called a multiple of p.

Quantitative Aptitude

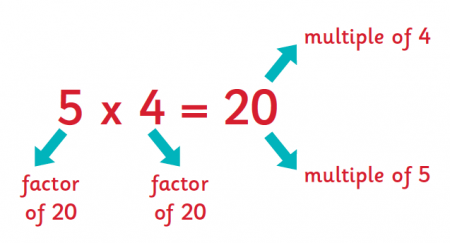
Common Multiple :
A number which is exactly divisible by all the given numbers is “Common multiple”.

Least Common Multiple (LCM) :
The least number which is exactly divisible by all the given numbers is LCM.

Common Factor:
A number which divides all the given numbers exactly is “Common factor”.
Highest Common Factor (HCF):
The greatest number that divides all the given numbers exactly is “HCF”.

H.C.F by Method of Prime Factors:

(1) H.C.F or G.C.F of 18 and 24?

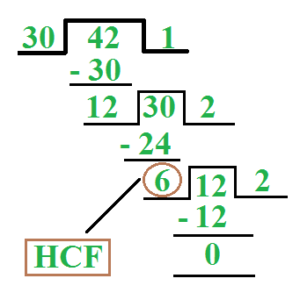
H.C.F by Method of Division:

(1) H.C.F of 30 and 42?

Problems on LCM and HCF

H.C.F and L.C.M of Fractions:

Co-primes: Two numbers are said to be co-primes if their H.C.F. is 1.

L.C.M and HCF Important Formulas

• Product of two numbers (First number x Second Number) = H.C.F. X L.C.M.
• H.C.F. of a given number always divides its L.C.M.
• To find the greatest number that will exactly divide x, y and z. Required number = HCF of x, y and z
• To find the Largest number that will divide x, y and z leaving remainders a, b and c respectively. Required number = HCF of (x -a), (y- b) and (z – c)
• To find the least number which is exactly divisible by x, y and z. Required number = LCM of x, y and z
• To find the least number which when divided by x, y and z leaves the remainders a, b and c respectively. It is always observed that, (x – a) = (y – b) = (z- c) = K (say).  Required number = (LCM of x, y and z) – K.
• To find the least number which, when divided by x, y and z leaves the same remainder r in each case. Required number = (LCM of x, y and z) + r
• To find the greatest number that will divide x, y and z leaving the same remainder ‘r’ in each case. Required number = HCF of (x -r), (y- r) and (z- r)
• Largest number which divides x, y, z to leave same remainder = H.C.F. of (y-x), (z-y), (z-x).
• HCF of two prime numbers is always 1.
• To find the n-digit greatest number which, when divided by x, y and z,
  (i) leaves no remainder (ie exactly divisible)
  Following step wise methods are adopted.
  Step I: LCM of x, y and z = L
  Step II: L) n-digit greatest number (
  Remainder (R)
  Step III: Required number = n – digit smallest number + (L – R)
  (ii) Leaves remainder K in each case
  Following step-wise method is adopted.
  Step I: LCM of x, y and z = L
  Step II: L) n-digit greatest number (
  Remainder (R)
  Step III: Required number = (n-digit greatest number – R) + K
• To find the n – digit smallest number which, when divided by x, y and z.(i) Leaves no remainder (i.e. exactly divisible)
  Following steps are followed.
  Step I: LCM of x, y and z = L
  Step II:  LCM) n-digit smallest number (
  Remainder (R)
  Step III: The required number = n-digit smallest number + (L – R)
  (ii) leaves remainder K in each case.
  Step I: LCM of x, y and z = L
  Step II:  LCM) n-digit smallest number (
  Remainder (R)
  Step III: Required number = n – digit smallest number + (L – R) + K
• To find the least number which on being divided by x, y and z leaves in each case a remiander R, but when divided by N leaves no remainder, following step-wise methods are adopted.
  Step I: Find the LCM of x, y and z say (L).
  Step II: Required number will be in the form of (LK + R); where K is a positive integer.
  Step III: N) L (Quotient (Q)
  —–
  Remainder (R₀)
  ∴  L = N X Q + R₀
  Now put the value of L into the expression obtained in step II.
  ∴ required number will be in the form of (N × Q + R₀) K + R
  or, (N × Q x K) + (R₀K + R)
  Clearly N x Q x K is always divisible by N.
  Step IV: Now make (R₀K + R) divisible by N by putting the least value of K. Say, 1, 2, 3, 4….
  Now put the value of K into the expression (LK + R) which will be the required number.
• There are n numbers. If the HCF of each pair is x and the LCM of all the n numbers is y, then the product of n numbers is given by  or Product of ‘n’ numbers = (HCF of each pair)^n-1 × (LCM of n numbers).