Simplification Questions, Formulas, Shortcuts and Practice Problems

Simplification Questions, Formulas, Shortcuts and Practice Problems

Rule of Simplification

• In simplifying an expression, first of all vinculum or bar must be removed. For example: we know that -4-5 = -9 but, –\(\overline{4-5}\) = -(- 1) = 1
• After removing the bar, the brackets must be removed, strictly in the order (), {} and [].
• After removing the brackets, we must use the following operations strictly in the order given below, (a) of (b) division (c) multiplication (d) addition and (e) subtraction

Quantitative Aptitude

Ex 1:

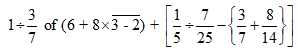
Solution:

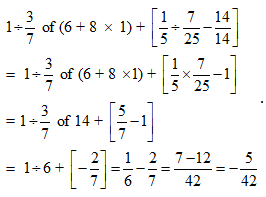
Simplification Questions on Application of Algebra Formulas

2. (a + b)² = a² + b² + 2ab

Ex 2: Simplify 0.46 x 0.46 + 0.54 x 0.54 + 0.92 x 0.54
Solution:
We have the expression
0.46 x 0.46 + 0.54 x 0.54 + 0.92 x 0.54 = (0.46)² + (0.54)² + 2. x 0.46 x 0.54
If we suppose a = 0.46 and b = 0.54, then
= a² + b² + 2ab = (a + b)²
= (0.46 + 0.54)² = (1.00)² = 1
∴ Answer = 1.

3. (a – b)² = a² +b² – 2ab

Ex 3. simplify 1.66 × 1.66 + 0.66 × 0.66 – 1.32 × 1.66
Solution:
We have the expression
1.66 × 1.66 + 0.66 × 0.66 – 1.32 × 1.66
Now, applying the above formula,
= (1.66 – 0.66)² = (1)² = 1
∴ Answer = 1

4. (a + b)² +(a- b)² = 2 (a² + b²)

Ex 4: Simplify the following
2[1.25 x 1.25 + 0.25 x 0.25]
Solution:
Applying the above formula, we have
2[(1.25)² + (0.25)² ] = (1.25 + 0.25)² + (1.25 – 0.25)²
= (1.5)²+ (1)²
= 2.25 + 1 = 3.25

5. (a + b)² – (a- b)² = 4ab

Ex 5:

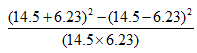
Solution:
Applying the above formula, we have a = 14.5, and b = 6.23

6. (a + b) (a – b) = a² –b²

Ex 6:
Simplify (50² – 40²) =? X 45
Solution:
Suppose a = 50 and b = 40
And required number = x
Applying the above formula,

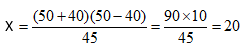
∴ Required answer = 20.

7. (a + b)³ = a³ + + 3a²b + 3ab² + b³ = a³ + b³ + 3ab (a + b)

Ex 7:
Simplify (0.6)³ + (0.4)³ + 3 x 0.6 x 0.4(0.6 + 0.4)
Solution:
The above expression can be written as
(0.6)³ + (0.4)³ + 3 x 0.6 x 0.4(0.6 + 0.4)
Now, we suppose 0.6 = a and 0.4 = b and applying the above formula, we have (0.6 + 0.4)³ = (1)³ = 1

8. (a – b)³ = a³ – 3a²b + 3ab² – b³ = a³ – b³ – 3ab (a-b)

Ex 8:
Simplify

Solution:

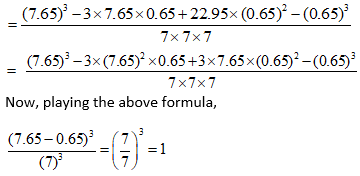
9. a³ +b³ = (a + b)(a² – ab + b²)

Solution:

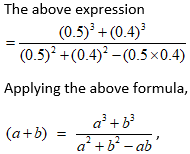
Here a = 0.5 and b = 0.4
∴ Required answer = 0.5 + 0.4 = 0.9

10. a³ – b³ = (a- b) (a² +ab + b²)

Ex 10:

Solution:

Simplification Questions – Practice Problems

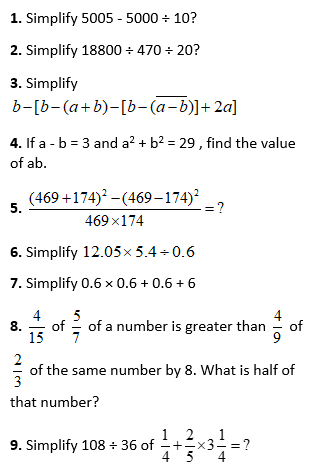
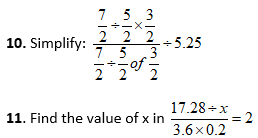
Simplification Practice Problems Answers

1. 4505
2. 2
3. 49
4. 10
5. 104
6. 108.45
7. 0.46
8. 315
9. \(13 \frac { 3 } { 10 }\)
10. \( \frac { 3 } { 7 }\)
11. 12
12. 2
13. \( \frac { 61 } { 11 }\)